NCERT Solutions for Polynomials
Exercise 2.1
1. The graphs of \( y = p(x) \) are given in Fig. 2.10 below, for some polynomials \( p(x) \). Find the number of zeroes of \( p(x) \), in each case.
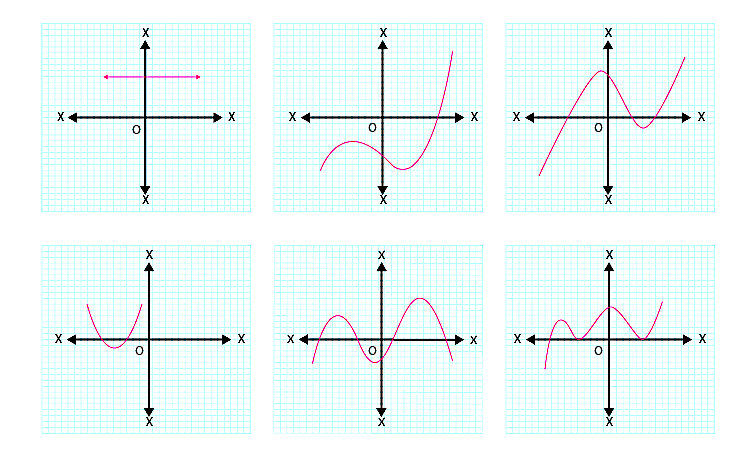
Solution:
To determine the number of zeroes of a polynomial \( p(x) \) from its graph, we use the graphical method:
Graphical Method to Find Zeroes:
- The total number of zeroes of a polynomial \( p(x) \) equals the total number of points where its graph intersects the x-axis.
- If the graph does not intersect the x-axis, the number of zeroes is \( 0 \).
(i)
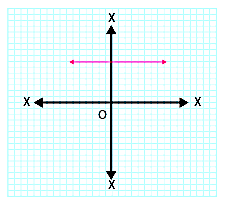
In the given graph, the curve is parallel to the x-axis and does not intersect it at any point.
Therefore, the number of zeroes of \( p(x) \) is \( 0 \).
(ii)
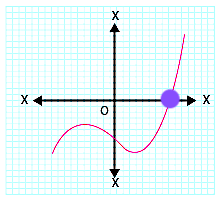
In the given graph, the curve intersects the x-axis at only one point.
Therefore, the number of zeroes of \( p(x) \) is \( 1 \).
(iii)
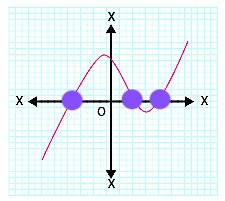
In the given graph, the curve intersects the x-axis at three distinct points.
Therefore, the number of zeroes of \( p(x) \) is \( 3 \).
(iv)
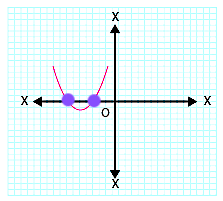
In the given graph, the curve intersects the x-axis at two points.
Therefore, the number of zeroes of \( p(x) \) is \( 2 \).
(v)
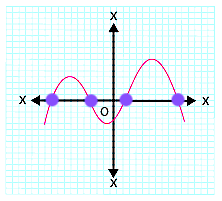
In the given graph, the curve intersects the x-axis at four points.
Therefore, the number of zeroes of \( p(x) \) is \( 4 \).
(vi)
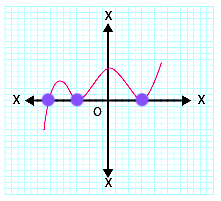
In the given graph, the curve intersects the x-axis at three distinct points.
Therefore, the number of zeroes of \( p(x) \) is \( 3 \).
― ― ― ― solutions by ncertbooks.net ― ― ― ―
Exercise 2.2
1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
Solution:
(i) \( x^2 – 2x – 8 \)
Factorizing the quadratic polynomial:
Start with the quadratic polynomial: \( x^2 – 2x – 8 \).
Break the middle term \(-2x\) into two terms such that their sum is \(-2\) and their product is equal to the product of the first and last coefficients (\(1 \times -8 = -8\)).
We can split \(-2x\) into \(-4x + 2x\) such that product of the first and last coefficients is \(-4 \times 2 = -8 \).
\( x^2 – 2x – 8 = x^2 – 4x + 2x – 8 \)
Group the terms in pairs for factoring: \( (x^2 – 4x) + (2x – 8) \).
Take the common factor from each group.
From \(x^2 – 4x\), take \(x\) as common: \( x(x – 4) \).
From \(2x – 8\), take \(2\) as common: \( 2(x – 4) \).
\( x^2 – 2x – 8 = x^2 – 4x + 2x – 8 \)
\( x^2 – 2x – 8 = (x^2 – 4x) + (2x – 8) \)
\( x^2 – 2x – 8 = x(x – 4) + 2(x – 4) \)
\( x^2 – 2x – 8 = (x – 4)(x + 2) \)
Therefore, the zeroes are \( 4 \) and \( -2 \).
Verification:
Sum of zeroes = \( 4 + (-2) = 2 \)
\(-\dfrac{\text{Coefficient of } x}{\text{Coefficient of } x^2} = -\frac{-2}{1} = 2 \) = Sum of zeroes
Product of zeroes = \( 4 \times (-2) = -8 \)
\( \dfrac{\text{Constant term}}{\text{Coefficient of } x^2} = \frac{-8}{1} = -8 \) = Product of zeroes
(ii) \( 4s^2 – 4s + 1 \)
Factorizing the quadratic polynomial:
Start with the quadratic polynomial: \( 4s^2 – 4s + 1 \).
Break the middle term \(-4s\) into two terms such that their sum is \(-4s\) and their product is equal to the product of the first and last coefficients (\(4 \times 1 = 4\)).
We can split \(-4s\) into \(-2s\) and \(-2s\) such that their product is \(-2 \times -2 = 4\).
\( 4s^2 – 4s + 1 = 4s^2 – 2s – 2s + 1 \)
Group the terms in pairs for factoring: \( (4s^2 – 2s) + (-2s + 1) \).
Take the common factor from each group.
From \(4s^2 – 2s\), take \(2s\) as common: \( 2s(2s – 1) \).
From \(-2s + 1\), take \(-1\) as common: \(-1(2s – 1) \).
\( 4s^2 – 4s + 1 = 2s(2s – 1) – 1(2s – 1) \)
\( 4s^2 – 4s + 1 = (2s – 1)(2s – 1) \)
Since the factors are identical, we have a repeated root. Therefore, the zeroes are \( \frac{1}{2} \) and \( \frac{1}{2} \).
Verification:
Sum of zeroes = \( \frac{1}{2} + \frac{1}{2} = 1 \)
\(-\frac{\text{Coefficient of } s}{\text{Coefficient of } s^2} = -\frac{-4}{4} = 1 \) = Sum of zeroes
Product of zeroes = \( \frac{1}{2} \times \frac{1}{2} = \frac{1}{4} \)
\( \frac{\text{Constant term}}{\text{Coefficient of } s^2} = \frac{1}{4} \) = Product of zeroes
(iii) \( 6x^2 – 3 – 7x \)
Rewriting the polynomial:
Rearrange the terms to write the polynomial in standard form: \( 6x^2 – 7x – 3 \).
Break the middle term \(-7x\) into two terms such that their sum is \(-7x\) and their product is equal to the product of the first and last coefficients (\(6 \times -3 = -18\)).
We can split \(-7x\) into \(-9x\) and \(2x\) such that their product is \(-9 \times 2 = -18\).
\( 6x^2 – 7x – 3 = 6x^2 – 9x + 2x – 3 \)
Group the terms in pairs for factoring: \( (6x^2 – 9x) + (2x – 3) \).
Take the common factor from each group.
From \(6x^2 – 9x\), take \(3x\) as common: \( 3x(2x – 3) \).
From \(2x – 3\), take \(1\) as common: \( 1(2x – 3) \).
\( 6x^2 – 7x – 3 = 3x(2x – 3) + 1(2x – 3) \)
\( 6x^2 – 7x – 3 = (3x + 1)(2x – 3) \)
Therefore, the zeroes are \( -\frac{1}{3} \) and \( \frac{3}{2} \).
Verification:
Sum of zeroes = \( -\dfrac{1}{3} + \dfrac{3}{2} = \dfrac{7}{6} \)
\( -\frac{\text{Coefficient of } x}{\text{Coefficient of } x^2} = -\frac{-7}{6} = \frac{7}{6} \) = Sum of zeroes
Product of zeroes = \( -\dfrac{1}{3} \times \dfrac{3}{2} = -\frac{1}{2} \)
\( \frac{\text{Constant term}}{\text{Coefficient of } x^2} = \frac{-3}{6} = -\frac{1}{2} \) = Product of zeroes
(iv) \( 4u^2 + 8u \)
Factorizing the polynomial:
Start with the polynomial: \( 4u^2 + 8u \).
Take the common factor from the terms. The greatest common factor of \( 4u^2 \) and \( 8u \) is \( 4u \).
\( 4u^2 + 8u = 4u(u + 2) \)
Therefore, the zeroes are \( 0 \) and \( -2 \).
Verification:
Sum of zeroes = \( 0 + (-2) = -2 \)
\( -\frac{\text{Coefficient of } u}{\text{Coefficient of } u^2} = -\frac{8}{4} = -2 \) = Sum of zeroes
Product of zeroes = \( 0 \times (-2) = 0 \)
\(\frac{\text{Constant term}}{\text{Coefficient of } u^2} = \frac{0}{4} = 0 \) = Product of zeroes
(v) \( t^2 – 15 \)
Rewriting the polynomial:
Start with the polynomial: \( t^2 – 15 \).
This is a difference of squares, which can be rewritten as:
\( t^2 – 15 = (t – \sqrt{15})(t + \sqrt{15}) \)
Solving for \( t \), we get:
\( t = \pm\sqrt{15} \)
Therefore, the zeroes are \( \sqrt{15} \) and \( -\sqrt{15} \).
Verification:
Sum of zeroes = \( \sqrt{15} + (-\sqrt{15}) = 0 \)
\( -\frac{\text{Coefficient of } t}{\text{Coefficient of } t^2} = -\frac{0}{1} = 0 \) = Sum of zeroes
Product of zeroes = \( \sqrt{15} \times (-\sqrt{15}) = -15 \)
\( \frac{\text{Constant term}}{\text{Coefficient of } t^2} = \frac{-15}{1} = -15 \) = Product of zeroes
(vi) \( 3x^2 – x – 4 \)
Factorizing the polynomial:
\( 3x^2 – x – 4 = 3x^2 – 4x + 3x – 4 = x(3x-4) + 1(3x-4) = (3x-4)(x+1) \)
Therefore, the zeroes are \( \frac{4}{3} \) and \( -1 \).
Verification:
Sum of zeroes = \( \frac{4}{3} + (-1) = \frac{1}{3} \)
\(\frac{-\text{Coefficient of } x}{\text{Coefficient of } x^2} = -\left(\frac{-1}{3}\right) = \frac{1}{3} \) = Sum of zeroes
Product of zeroes: \( \frac{4}{3} \times (-1) = -\frac{4}{3} \)
\( \frac{\text{Constant term}}{\text{Coefficient of } x^2} = -\frac{4}{3} \) = Product of zeroes
― ― ― ― solutions by ncertbooks.net ― ― ― ―
2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes, respectively.
Solution:
(i) \( \frac{1}{4}, -1 \)
From the formulas of sum and product of zeroes, we know:
Sum of zeroes = \( \alpha + \beta = \frac{1}{4} \)
Product of zeroes = \( \alpha \beta = -1 \)
If \( \alpha \) and \( \beta \) are zeroes of any quadratic polynomial, the polynomial can be written as:
\( x^2 – (\alpha + \beta)x + \alpha \beta = 0 \)
\( x^2 – \left(\frac{1}{4}\right)x + (-1) = 0 \)
\( 4x^2 – x – 4 = 0 \)
Thus, \( 4x^2 – x – 4 \) is the quadratic polynomial for given sum and product of zeroes.
(ii) \( \sqrt{2}, \frac{1}{3} \)
From the formulas of sum and product of zeroes, we know:
Sum of zeroes = \( \alpha + \beta = \sqrt{2} \)
Product of zeroes = \( \alpha \beta = \frac{1}{3} \)
If \( \alpha \) and \( \beta \) are zeroes of any quadratic polynomial, the polynomial can be written as:
\( x^2 – (\alpha + \beta)x + \alpha \beta = 0 \)
\( x^2 – (\sqrt{2})x + \frac{1}{3} = 0 \)
\( 3x^2 – 3\sqrt{2}x + 1 = 0 \)
Thus, \( 3x^2 – 3\sqrt{2}x + 1 \) is the quadratic polynomial for given sum and product of zeroes.
(iii) \( 0, \sqrt{5} \)
From the formulas of sum and product of zeroes, we know:
Sum of zeroes = \( \alpha + \beta = 0 \)
Product of zeroes = \( \alpha \beta = \sqrt{5} \)
If \( \alpha \) and \( \beta \) are zeroes of any quadratic polynomial, the polynomial can be written as:
\( x^2 – (\alpha + \beta)x + \alpha \beta = 0 \)
\( x^2 – (0)x + \sqrt{5} = 0 \)
\( x^2 + \sqrt{5} = 0 \)
Thus, \( x^2 + \sqrt{5} \) is the quadratic polynomial for given sum and product of zeroes.
(iv) \( 1, 1 \)
From the formulas of sum and product of zeroes, we know:
Sum of zeroes = \( \alpha + \beta = 1 \)
Product of zeroes = \( \alpha \beta = 1 \)
If \( \alpha \) and \( \beta \) are zeroes of any quadratic polynomial, the polynomial can be written as:
\( x^2 – (\alpha + \beta)x + \alpha \beta = 0 \)
\( x^2 – (1)x + 1 = 0 \)
\( x^2 – x + 1 = 0 \)
Thus, \( x^2 – x + 1 \) is the quadratic polynomial for given sum and product of zeroes.
(v) \( -\frac{1}{4}, \frac{1}{4} \)
From the formulas of sum and product of zeroes, we know:
Sum of zeroes = \( \alpha + \beta = -\frac{1}{4} \)
Product of zeroes = \( \alpha \beta = \frac{1}{4} \)
If \( \alpha \) and \( \beta \) are zeroes of any quadratic polynomial, the polynomial can be written as:
\( x^2 – (\alpha + \beta)x + \alpha \beta = 0 \)
\( x^2 – \left(-\frac{1}{4}\right)x + \frac{1}{4} = 0 \)
\( 4x^2 + x + 1 = 0 \)
Thus, \( 4x^2 + x + 1 \) is the quadratic polynomial for given sum and product of zeroes.
(vi) \( 4, 1 \)
From the formulas of sum and product of zeroes, we know:
Sum of zeroes = \( \alpha + \beta = 4 \)
Product of zeroes = \( \alpha \beta = 1 \)
If \( \alpha \) and \( \beta \) are zeroes of any quadratic polynomial, the polynomial can be written as:
\( x^2 – (\alpha + \beta)x + \alpha \beta = 0 \)
\( x^2 – (4)x + 1 = 0 \)
\( x^2 – 4x + 1 = 0 \)
Thus, \( x^2 – 4x + 1 \) is the quadratic polynomial for given sum and product of zeroes.
― ― ― ― solutions by ncertbooks.net ― ― ― ―
Exercise 2.3
1. Divide the polynomial \( p(x) \) by the polynomial \( g(x) \) and find the quotient and remainder in each of the following:
Solution:
(i) \( p(x) = x^3 – 3x^2 + 5x – 3, \ g(x) = x^2 – 2 \)
Given:
Dividend, \( p(x) = x^3 – 3x^2 + 5x – 3 \)
Divisor, \( g(x) = x^2 – 2 \)
Using polynomial long division:

Result:
Quotient, \( Q(x) = x – 3 \)
Remainder, \( R(x) = 7x – 9 \)
(ii) \( p(x) = x^4 – 3x^2 + 4x + 5, \ g(x) = x^2 + 1 – x \)
Given:
Dividend, \( p(x) = x^4 – 3x^2 + 4x + 5 \)
Divisor, \( g(x) = x^2 + 1 – x \)
Using polynomial long division:
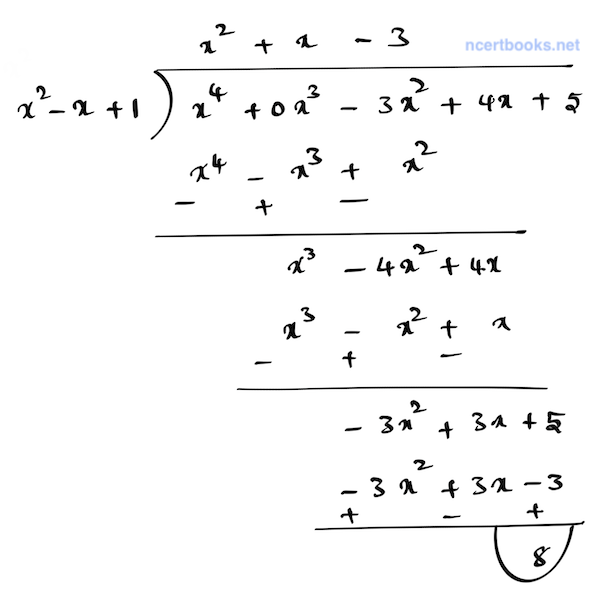
Result:
Quotient, \( Q(x) = x^2 + x – 3 \)
Remainder, \( R(x) = 8 \)
(iii) \( p(x) = x^4 – 5x + 6, \ g(x) = 2 – x^2 \)
Given:
Dividend, \( p(x) = x^4 – 5x + 6 = x^4 + 0x^2 – 5x + 6 \)
Divisor, \( g(x) = 2 – x^2 = -x^2 + 2 \)
Using polynomial long division:
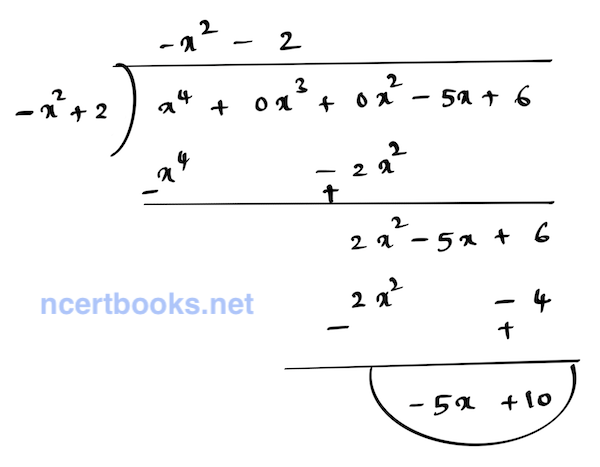
Result:
Quotient, \( Q(x) = -x^2 – 2 \)
Remainder, \( R(x) = -5x + 10 \)
― ― ― ― solutions by ncertbooks.net ― ― ― ―
2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
Solution:
(i) \( t^2 – 3 \), \( 2t^4 + 3t^3 – 2t^2 – 9t – 12 \)
Given:
First polynomial (divisor): \( t^2 – 3 \)
Second polynomial (dividend): \( 2t^4 + 3t^3 – 2t^2 – 9t – 12 \)
Using polynomial long division:

Result:
Remainder, \( R(x) = 0 \)
Since the remainder is \( 0 \), \( t^2 – 3 \) is a factor of \( 2t^4 + 3t^3 – 2t^2 – 9t – 12 \).
(ii) \( x^2 + 3x + 1 \), \( 3x^4 + 5x^3 – 7x^2 + 2x + 2 \)
Given:
First polynomial (divisor): \( x^2 + 3x + 1 \)
Second polynomial (dividend): \( 3x^4 + 5x^3 – 7x^2 + 2x + 2 \)
Using polynomial long division (refer to the image for detailed steps):
Result:
Remainder, \( R(x) = 0 \)
Since the remainder is \( 0 \), \( x^2 + 3x + 1 \) is a factor of \( 3x^4 + 5x^3 – 7x^2 + 2x + 2 \).
(iii) \( x^3 – 3x + 1 \), \( x^5 – 4x^3 + x^2 + 3x + 1 \)
Given:
First polynomial (divisor): \( x^3 – 3x + 1 \)
Second polynomial (dividend): \( x^5 – 4x^3 + x^2 + 3x + 1 \)
Using polynomial long division (refer to the image for detailed steps):
Result:
Remainder, \( R(x) \neq 0 \)
Since the remainder is not \( 0 \), \( x^3 – 3x + 1 \) is not a factor of \( x^5 – 4x^3 + x^2 + 3x + 1 \).
― ― ― ― solutions by ncertbooks.net ― ― ― ―
3. Obtain all other zeroes of \( 3x^4 + 6x^3 – 2x^2 – 10x – 5 \), if two of its zeroes are \( \sqrt{\frac{5}{3}} \) and \( -\sqrt{\frac{5}{3}} \).
Solution:
The given polynomial is \( f(x) = 3x^4 + 6x^3 – 2x^2 – 10x – 5 \), which is a polynomial of degree 4. A polynomial of degree 4 has exactly 4 roots (zeroes).
Two of the zeroes are given as \( \sqrt{\frac{5}{3}} \) and \( -\sqrt{\frac{5}{3}} \). Since these two are conjugate roots, we can construct their factor:
Factor: \( (x – \sqrt{\frac{5}{3}})(x + \sqrt{\frac{5}{3}}) = x^2 – \frac{5}{3} \)
To eliminate the fraction, multiply by \( 3 \):
Factor: \( 3x^2 – 5 \)
Thus, \( 3x^2 – 5 \) is a factor of \( f(x) \). Now, divide \( f(x) \) by \( 3x^2 – 5 \) to find the other factor.
Using polynomial long division (refer to image for detailed steps), we divide:
\( f(x) = (3x^2 – 5)(x^2 + 2x + 1) \)
Now, factorize the quadratic polynomial \( x^2 + 2x + 1 \):
Factorizing \( x^2 + 2x + 1 \):
\( x^2 + 2x + 1 = (x + 1)(x + 1) = (x + 1)^2 \)
Thus, the complete factorization of \( f(x) \) is:
\( f(x) = (3x^2 – 5)(x + 1)^2 \)
Finding all zeroes:
The zeroes of \( 3x^2 – 5 \) are:
\( x = \pm\sqrt{\frac{5}{3}} \)
The zeroes of \( (x + 1)^2 \) are:
\( x = -1 \), \( x = -1 \)
Conclusion:
The four zeroes of the polynomial \( f(x) = 3x^4 + 6x^3 – 2x^2 – 10x – 5 \) are:
\( \sqrt{\frac{5}{3}}, -\sqrt{\frac{5}{3}}, -1, -1 \)
― ― ― ― solutions by ncertbooks.net ― ― ― ―
4. On dividing \( x^3 – 3x^2 + x + 2 \) by a polynomial \( g(x) \), the quotient and remainder were \( x – 2 \) and \( -2x + 4 \), respectively. Find \( g(x) \).
Solution:
Given:
Dividend, \( p(x) = x^3 – 3x^2 + x + 2 \)
Quotient, \( q(x) = x – 2 \)
Remainder, \( r(x) = -2x + 4 \)
We are tasked to find the divisor, \( g(x) \).
Using the division algorithm:
Dividend = Divisor × Quotient + Remainder
\( p(x) = g(x) \cdot q(x) + r(x) \)
Substituting the given values:
\( x^3 – 3x^2 + x + 2 = g(x) \cdot (x – 2) + (-2x + 4) \)
Rearranging to isolate \( g(x) \):
\( x^3 – 3x^2 + x + 2 – (-2x + 4) = g(x) \cdot (x – 2) \)
\( g(x) \cdot (x – 2) = x^3 – 3x^2 + 3x – 2 \)
Now, divide \( x^3 – 3x^2 + 3x – 2 \) by \( x – 2 \) to find \( g(x) \):
Using polynomial long division (refer to image for detailed steps):
Result:
\( g(x) = x^2 – x + 1 \)
Final Answer:
The divisor is \( g(x) = x^2 – x + 1 \).
― ― ― ― solutions by ncertbooks.net ― ― ― ―
5. Give examples of polynomials \( p(x) \), \( g(x) \), \( q(x) \), and \( r(x) \), which satisfy the division algorithm and:
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
According to the division algorithm, for any two polynomials \( p(x) \) (dividend) and \( g(x) \) (divisor), where \( g(x) \neq 0 \), we can write:
\( p(x) = g(x) \cdot q(x) + r(x) \)
where, \( r(x) = 0 \) or \( \text{deg } r(x) < \text{deg } g(x) \).
(i) \( \text{deg } p(x) = \text{deg } q(x) \)
Condition: The degree of the dividend \( p(x) \) is equal to the degree of the quotient \( q(x) \). This happens when the divisor \( g(x) \) is a constant term.
Example:
Let \( p(x) = 3x^2 + 3x + 3 \), \( g(x) = 3 \).
Dividing \( p(x) \) by \( g(x) \):
\( (3x^2 + 3x + 3) / 3 = x^2 + x + 1 = q(x) \)
Result:
The degree of \( q(x) = 2 \), which is equal to the degree of \( p(x) \).
Hence, the division algorithm is satisfied.
(ii) \( \text{deg } q(x) = \text{deg } r(x) \)
Condition: The degree of the quotient \( q(x) \) is equal to the degree of the remainder \( r(x) \).
Example:
Let
\( p(x) = x^2 + 3 \)
\( g(x) = x – 1 \).
Dividing \( p(x) \) by \( g(x) \):
\( x^2 + 3 = (x – 1) \cdot (x) + (x + 3) \)
Result:
The degree of \( q(x) = 1 \), and the degree of \( r(x) = 1 \). Thus, \( \text{deg } q(x) = \text{deg } r(x) \).
Hence, the division algorithm is satisfied.
(iii) \( \text{deg } r(x) = 0 \)
Condition: The degree of the remainder \( r(x) \) is zero. This happens when the remainder is a constant term.
Example:
Let \( p(x) = x^2 + 1 \), \( g(x) = x \).
Dividing \( p(x) \) by \( g(x) \):
\( x^2 + 1 = (x) \cdot (x) + 1 \)
Result:
The degree of \( r(x) = 0 \), as \( r(x) = 1 \), a constant term.
Hence, the division algorithm is satisfied.
― ― ― ― solutions by ncertbooks.net ― ― ― ―
Exercise 2.4
1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
Solution:
(i) \( 2x^3 + x^2 – 5x + 2; \ -\frac{1}{2}, 1, -2 \)
Given:
\( p(x) = 2x^3 + x^2 – 5x + 2 \)
Zeroes: \( \alpha = -\frac{1}{2}, \ \beta = 1, \ \gamma = -2 \)
Step 1: Verify zeroes:
Substitute each zero into the polynomial:
\( p\left(-\frac{1}{2}\right) = 2\left(-\frac{1}{2}\right)^3 + \left(-\frac{1}{2}\right)^2 – 5\left(-\frac{1}{2}\right) + 2 = 0 \)
\( p(1) = 2(1)^3 + (1)^2 – 5(1) + 2 = 0 \)
\( p(-2) = 2(-2)^3 + (-2)^2 – 5(-2) + 2 = 0 \)
Since \( p(x) = 0 \) for all given values, the numbers are indeed the zeroes of the polynomial.
Step 2: Verify relationships between zeroes and coefficients:
Comparing \( p(x) = 2x^3 + x^2 – 5x + 2 \) with \( ax^3 + bx^2 + cx + d \), we get:
\( a = 2, \ b = 1, \ c = -5, \ d = 2 \)
Using the relationships:
\( \alpha + \beta + \gamma = -\frac{1}{2} + 1 – 2 = -\frac{1}{2} = -\frac{b}{a} = -\frac{1}{2} \)
\( \alpha\beta + \beta\gamma + \gamma\alpha = \left(-\frac{1}{2} \cdot 1\right) + \left(1 \cdot -2\right) + \left(-2 \cdot -\frac{1}{2}\right) = -\frac{5}{2} = \frac{c}{a} \)
\( \alpha\beta\gamma = \left(-\frac{1}{2}\right) \cdot 1 \cdot -2 = -2/2 = -\frac{d}{a} \)
The relationships are verified.
Conclusion: The zeroes and their relationships with the coefficients are verified.
(ii) \( x^3 – 4x^2 + 5x – 2; \ 2, 1, 1 \)
Given:
\( p(x) = x^3 – 4x^2 + 5x – 2 \)
Zeroes: \( \alpha = 2, \ \beta = 1, \ \gamma = 1 \)
Step 1: Verify zeroes:
Substitute each zero into the polynomial:
\( p(2) = (2)^3 – 4(2)^2 + 5(2) – 2 = 0 \)\( p(1) = (1)^3 – 4(1)^2 + 5(1) – 2 = 0 \)
Since \( p(x) = 0 \) for all given values, the numbers are indeed the zeroes of the polynomial.
Step 2: Verify relationships between zeroes and coefficients:
Comparing \( p(x) = x^3 – 4x^2 + 5x – 2 \) with \( ax^3 + bx^2 + cx + d \), we get:
\( a = 1, \ b = -4, \ c = 5, \ d = -2 \)
Using the relationships:
\( \alpha + \beta + \gamma = 2 + 1 + 1 = 4 = -\frac{b}{a} = -\frac{-4}{1} \)
\( \alpha\beta + \beta\gamma + \gamma\alpha = (2 \cdot 1) + (1 \cdot 1) + (1 \cdot 2) = 5 = \frac{c}{a} \)
\( \alpha\beta\gamma = (2 \cdot 1 \cdot 1) = 2 = -\frac{d}{a} = -\frac{-2}{1} \)
The relationships are verified.
Conclusion: The zeroes and their relationships with the coefficients are verified.
― ― ― ― solutions by ncertbooks.net ― ― ― ―
2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as \( 2, -7, -14 \), respectively.
Solution:
Let the cubic polynomial be \( p(x) = ax^3 + bx^2 + cx + d \), and let its zeroes be \( \alpha, \beta, \gamma \).
From the given conditions:
Sum of zeroes, \( \alpha + \beta + \gamma = -\frac{b}{a} = 2 \)
Sum of the product of zeroes taken two at a time, \( \alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a} = -7 \)
Product of zeroes, \( \alpha\beta\gamma = -\frac{d}{a} = -14 \)
Assuming \( a = 1 \), substitute the values into the expressions for the coefficients:
\( b = -a \cdot (\alpha + \beta + \gamma) = -1 \cdot 2 = -2 \)
\( c = a \cdot (\alpha\beta + \beta\gamma + \gamma\alpha) = 1 \cdot (-7) = -7 \)
\( d = -a \cdot (\alpha\beta\gamma) = -1 \cdot (-14) = 14 \)
Substitute the values of \( a, b, c, \) and \( d \) into the general cubic polynomial:
\( p(x) = x^3 – 2x^2 – 7x + 14 \)
Final Answer: The cubic polynomial is:
\( p(x) = x^3 – 2x^2 – 7x + 14 \)
― ― ― ― solutions by ncertbooks.net ― ― ― ―
3. If the zeroes of the polynomial \( x^3 – 3x^2 + x + 1 \) are \( a – b \), \( a \), and \( a + b \), find \( a \) and \( b \).
Solution:
The given polynomial is:
\( p(x) = x^3 – 3x^2 + x + 1 \)
The zeroes are given as \( a – b \), \( a \), and \( a + b \).
Comparing \( p(x) = x^3 – 3x^2 + x + 1 \) with the general cubic polynomial \( px^3 + qx^2 + rx + s \), we get:
\( p = 1, \ q = -3, \ r = 1, \ s = 1 \)
Step 1: Use the sum of the zeroes:
The sum of the zeroes of a cubic polynomial is given by:
\( \alpha + \beta + \gamma = -\frac{q}{p} \)
Substitute \( \alpha = a – b \), \( \beta = a \), \( \gamma = a + b \):
\( (a – b) + a + (a + b) = 3a \)
\( -\frac{q}{p} = -\frac{-3}{1} = 3 \)
\( 3a = 3 \)
\( a = 1 \)
Thus, the zeroes are \( 1 – b \), \( 1 \), and \( 1 + b \).
Step 2: Use the product of the zeroes:
The product of the zeroes of a cubic polynomial is given by:
\( \alpha \beta \gamma = -\frac{s}{p} \)
Substitute \( \alpha = 1 – b \), \( \beta = 1 \), \( \gamma = 1 + b \):
\( (1 – b)(1)(1 + b) = 1 – b^2 \)
\( -\frac{s}{p} = -\frac{1}{1} = -1 \)
\( 1 – b^2 = -1 \)
\( b^2 = 1 + 1 = 2 \)
\( b = \pm\sqrt{2} \)
Final Answer:
The zeroes of the polynomial are \( 1 – \sqrt{2}, 1, \text{ and } 1 + \sqrt{2} \).
― ― ― ― solutions by ncertbooks.net ― ― ― ―
4. If two zeroes of the polynomial \( x^4 – 6x^3 – 26x^2 + 138x – 35 \) are \( 2 \pm \sqrt{3} \), find the other zeroes.
Solution:
The given polynomial is:
\( f(x) = x^4 – 6x^3 – 26x^2 + 138x – 35 \)
We are given two zeroes: \( 2 + \sqrt{3} \) and \( 2 – \sqrt{3} \). Since this is a degree 4 polynomial, it has four zeroes in total.
Step 1: Find the quadratic factor corresponding to the given zeroes:
The product of the factors corresponding to the zeroes \( 2 + \sqrt{3} \) and \( 2 – \sqrt{3} \) is:
\( \left(x – (2 + \sqrt{3})\right)\left(x – (2 – \sqrt{3})\right) = x^2 – 4x + 1 \)
Thus, \( x^2 – 4x + 1 \) is a factor of \( f(x) \).
Step 2: Divide \( f(x) \) by \( x^2 – 4x + 1 \):
Using polynomial long division (refer to the image for detailed steps), we divide:
\( f(x) = (x^2 – 4x + 1)(x^2 – 2x – 35) \)
Step 3: Factorize \( x^2 – 2x – 35 \):
Factorize \( x^2 – 2x – 35 \) as follows:
\( x^2 – 2x – 35 = x^2 – 7x + 5x – 35 = x(x – 7) + 5(x – 7) \)
\( x^2 – 2x – 35 = (x + 5)(x – 7) \)
Step 4: Write all zeroes:
The zeroes of \( x^2 – 4x + 1 \) are \( 2 + \sqrt{3} \) and \( 2 – \sqrt{3} \).
The zeroes of \( x^2 – 2x – 35 \) are \( -5 \) and \( 7 \).
Final Answer:
The zeroes of the polynomial are: \( 2 + \sqrt{3}, 2 – \sqrt{3}, -5, \text{ and } 7 \).
― ― ― ― solutions by ncertbooks.net ― ― ― ―
